Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

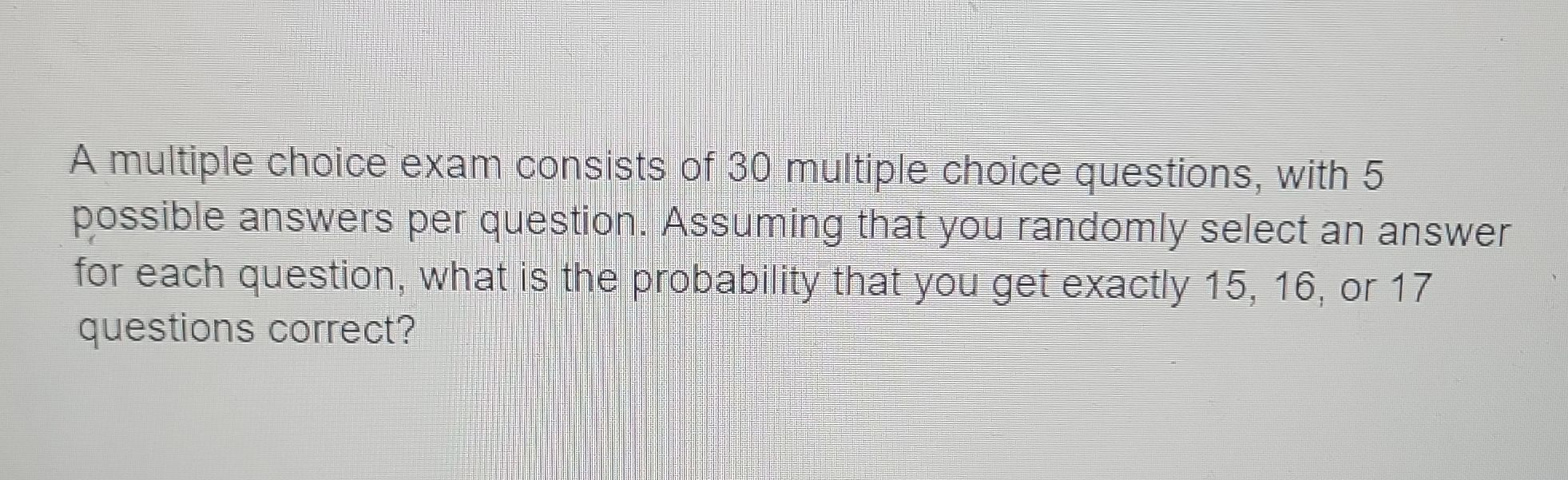
A multiple choice exam consists of 30 multiple choice questions, with 5 possible answers per question. Assuming that you randomly select an answer for each question, what is the probability that you get exactly 15,16 , or 17 questions correct?

A multiple choice exam consists of 3030 multiple choice questions, with 55 possible answers per question. Assuming that you randomly select an answer for each question, what is the probability that you get exactly 1515,1616 , or 1717 questions correct?

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 8right chevron icon
Probability of simple eventsright chevron icon

Full solution

Q. A multiple choice exam consists of 3030 multiple choice questions, with 55 possible answers per question. Assuming that you randomly select an answer for each question, what is the probability that you get exactly 1515,1616 , or 1717 questions correct?
  1. Understand the problem: Understand the problem and determine the formula to use.\newlineWe need to calculate the probability of getting exactly 1515, 1616, or 1717 questions correct out of 3030 when each question has 55 possible answers. The probability of getting a question right by random guessing is 15\frac{1}{5}, and the probability of getting it wrong is 45\frac{4}{5}. We will use the binomial probability formula:\newlineP(X=k)=(nk)⋅(pk)⋅((1−p)(n−k))P(X = k) = \binom{n}{k} \cdot (p^k) \cdot ((1-p)^{(n-k)})\newlinewhere nn is the number of trials (questions), kk is the number of successes (correct answers), and 161600 is the probability of success on a single trial.
  2. Calculate probability of 1515: Calculate the probability of getting exactly 1515 questions correct.\newlineUsing the binomial formula:\newlineP(X=15)=(3015)⋅(15)15⋅(45)30−15P(X = 15) = \binom{30}{15} \cdot \left(\frac{1}{5}\right)^{15} \cdot \left(\frac{4}{5}\right)^{30-15}\newlineWe calculate (3015)\binom{30}{15} using the combination formula n!/(k!(n−k)!)n! / (k!(n-k)!):\newline(3015)=30!(15!⋅15!)\binom{30}{15} = \frac{30!}{(15! \cdot 15!)}\newlineNow we calculate the probability:\newlineP(X=15)=30!(15!⋅15!)⋅(15)15⋅(45)15P(X = 15) = \frac{30!}{(15! \cdot 15!)} \cdot \left(\frac{1}{5}\right)^{15} \cdot \left(\frac{4}{5}\right)^{15}
  3. Calculate probability of 1616: Calculate the probability of getting exactly 1616 questions correct.\newlineUsing the binomial formula:\newlineP(X=16)=(3016)⋅(15)16⋅(45)30−16P(X = 16) = \binom{30}{16} \cdot \left(\frac{1}{5}\right)^{16} \cdot \left(\frac{4}{5}\right)^{30-16}\newlineWe calculate (3016)\binom{30}{16} using the combination formula n!/(k!(n−k)!)n! / (k!(n-k)!):\newline(3016)=30!16!⋅14!\binom{30}{16} = \frac{30!}{16! \cdot 14!}\newlineNow we calculate the probability:\newlineP(X=16)=30!16!⋅14!⋅(15)16⋅(45)14P(X = 16) = \frac{30!}{16! \cdot 14!} \cdot \left(\frac{1}{5}\right)^{16} \cdot \left(\frac{4}{5}\right)^{14}
  4. Calculate probability of 1717: Calculate the probability of getting exactly 1717 questions correct.\newlineUsing the binomial formula:\newlineP(X=17)=(3017)⋅(15)17⋅(45)30−17P(X = 17) = \binom{30}{17} \cdot \left(\frac{1}{5}\right)^{17} \cdot \left(\frac{4}{5}\right)^{30-17}\newlineWe calculate (3017)\binom{30}{17} using the combination formula n!/(k!(n−k)!)n! / (k!(n-k)!):\newline(3017)=30!17!⋅13!\binom{30}{17} = \frac{30!}{17! \cdot 13!}\newlineNow we calculate the probability:\newlineP(X=17)=30!17!⋅13!⋅(15)17⋅(45)13P(X = 17) = \frac{30!}{17! \cdot 13!} \cdot \left(\frac{1}{5}\right)^{17} \cdot \left(\frac{4}{5}\right)^{13}
  5. Add probabilities: Add the probabilities of getting exactly 1515, 1616, and 1717 questions correct to find the total probability.\newlineP(15,16, or 17 correct)=P(X=15)+P(X=16)+P(X=17)P(15, 16, \text{ or } 17 \text{ correct}) = P(X = 15) + P(X = 16) + P(X = 17)\newlineWe add the probabilities calculated in steps 22, 33, and 44.
  6. Perform calculations: Perform the calculations and simplify the result.\newlineThis step involves actual numerical computation, which typically requires a calculator or computer software, as the factorials and powers involved are too large for manual calculation. However, the process has been described correctly in the previous steps.

More problems from Probability of simple events

Question
You roll a 66-sided die two times. What is the probability of rolling a number greater than \(3\) and then rolling a number less than \(4\)? Write your answer as a percentage. \newline____ `%`
Get tutor helpright-arrow

Posted 5 months ago

Question
There are 99 college students running for student government class president. The candidates include 77 education majors.\newlineIf 66 of the candidates are randomly chosen to give the first 66 speeches, what is the probability that all of them are education majors?\newlineWrite your answer as a decimal rounded to four decimal places.
Get tutor helpright-arrow

Posted 8 months ago

Question
In an experiment, the probability that event A A occurs is 27 \frac{2}{7} , the probability that event B B occurs is 79 \frac{7}{9} , and the probability that events A A and B B both occur is 19 \frac{1}{9} .\newlineAre A A and B B independent events?\newlineChoices:\newline(A) yes\text{yes}\newline(B) no\text{no}
Get tutor helpright-arrow

Posted 8 months ago

Question
At a science museum, visitors can compete to see who has a faster reaction time. Competitors watch a red screen, and the moment they see it turn from red to green, they push a button. The machine records their reaction times and also asks competitors to report their gender.\newlineThe probability that a competitor reacted in over 0.70.7 seconds is 0.60.6, the probability that a competitor was female is 0.40.4, and the probability that a competitor reacted in over 0.70.7 seconds and was female is 0.30.3.\newlineWhat is the probability that a randomly chosen competitor reacted in over 0.70.7 seconds or was female?\newlineWrite your answer as a whole number, decimal, or simplified fraction.\newline______
Get tutor helpright-arrow

Posted 8 months ago

Question
A restaurant server claims that \(28\)% of the time he leaves candy with the bill, the customer tips well. \newlineIf the server's claim is true, and one day he leaves candy with \(4\) customers' bills, what is the probability that exactly \(3\) of those customers will tip well?\newlineWrite your answer as a decimal rounded to the nearest thousandth.
Get tutor helpright-arrow

Posted 7 months ago

Question
There is a spinner with `50` equally likely sections, numbered from `1` to `50`. You have the opportunity to spin it. If the number is odd, you win $`11`. If the number is even, you win nothing. If you play the game, what is the expected payoff?\(\$\)_____
Get tutor helpright-arrow

Posted 8 months ago

Question
There are two different raffles you can enter.\newlineIn raffle A, one ticket will win a `$720` prize, and the other tickets will win nothing. There are 1,0001,000 in the raffle, each costing `$11`.\newlineRaffle B is for a `$370` prize. Out of 125125 tickets, each costing `$5`, one ticket will win the prize, and the other tickets will win nothing.\newlineWhich raffle is a better deal?\newlineChoices:\newline[A]Raffle A\text{[A]Raffle A}\newline[B]Raffle B\text{[B]Raffle B}
Get tutor helpright-arrow

Posted 8 months ago

Question
XX is a normally distributed random variable with mean 4949 and standard deviation 2525.\newlineWhat is the probability that XX is between 2424 and 7474??\newlineUse the 0.68−0.95−0.9970.68-0.95-0.997 rule and write your answer as a decimal. Round to the nearest thousandth if necessary.\newline____
Get tutor helpright-arrow

Posted 8 months ago

Question
XX is a normally distributed random variable with mean 6565 and standard deviation 88.\newlineWhat is the probability that XX is between 6262 and 6868??\newlineWrite your answer as a decimal rounded to the nearest thousandth.\newline____
Get tutor helpright-arrow

Posted 8 months ago

Question
Complete the statement. Round your answer to the nearest thousandth.\newlineIn a population that is normally distributed with mean 4343 and standard deviation 33, the bottom 30%30\% of the values are those less than ______.
Get tutor helpright-arrow

Posted 8 months ago

View all (20)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant