Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

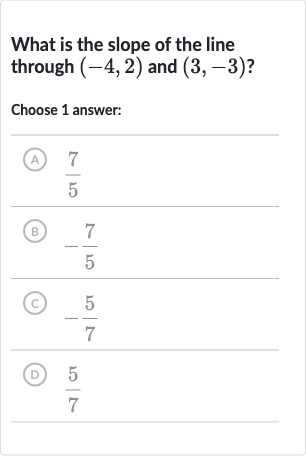
What is the slope of the line through (-4,2) and (3,-3) ? Choose 1 answer: (A) (7)/(5) (B) -(7)/(5) (c) -(5)/(7) (D) (5)/(7)

What is the slope of the line through (−4,2)(-4,2) and (3,−3)(3,-3)? Choose 11 answer: (A) 75\frac{7}{5} (B) −75-\frac{7}{5} (C) −57-\frac{5}{7} (D) 57\frac{5}{7}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Find the slope from two pointsright chevron icon

Full solution

Q. What is the slope of the line through (−4,2)(-4,2) and (3,−3)(3,-3)? Choose 11 answer: (A) 75\frac{7}{5} (B) −75-\frac{7}{5} (C) −57-\frac{5}{7} (D) 57\frac{5}{7}
  1. Identify the slope formula: Identify the slope formula.\newlineThe slope of a line through two points (x1,y1)(x_1, y_1) and (x2,y2)(x_2, y_2) is given by the formula:\newlineSlope = y2−y1x2−x1\frac{y_2 - y_1}{x_2 - x_1}
  2. Substitute the given points: Substitute the given points into the slope formula.\newlineWe have the points (−4,2)(-4, 2) and (3,−3)(3, -3). Let's denote (−4,2)(-4, 2) as (x1,y1)(x_1, y_1) and (3,−3)(3, -3) as (x2,y2)(x_2, y_2).\newlineSo, x1=−4x_1 = -4, y1=2y_1 = 2, x2=3x_2 = 3, and y2=−3y_2 = -3.\newlineSlope = (3,−3)(3, -3)00
  3. Perform the subtraction: Perform the subtraction in the numerator and the denominator.\newlineNumerator: −3−2=−5-3 - 2 = -5\newlineDenominator: 3−(−4)=3+4=73 - (-4) = 3 + 4 = 7\newlineSlope = −57\frac{-5}{7}
  4. Determine the correct answer: Determine the correct answer from the given options.\newlineThe slope we calculated is −57-\frac{5}{7}, which corresponds to option (C) −(57)-\left(\frac{5}{7}\right).

More problems from Find the slope from two points

Question
What is the slope of the line through (−2,−6)(-2,-6) and (2,2)(2,2)?\newlineChoose 11 answer:\newline(A) 12\frac{1}{2}\newline(B) −2-2\newline(C) 22\newline(D) −12-\frac{1}{2}
Get tutor helpright-arrow

Posted 4 months ago

Question
What is the slope of the line through (−10,1)(-10,1) and (0,−4)(0,-4)? Choose 11 answer: \newline(A) 22 \newline(B) 12\frac{1}{2} \newline(C) −12-\frac{1}{2} \newline(D) −2-2
Get tutor helpright-arrow

Posted 4 months ago

Question
What is the slope of the line through (−9,−6)(-9,-6) and (3,−9)(3,-9)? Choose 11 answer: \newline(A) −4-4 \newline(B) 14\frac{1}{4} \newline(C) 44 \newline(D) −14-\frac{1}{4}
Get tutor helpright-arrow

Posted 4 months ago

Question
What is the slope of the line through \newline(−5,−10)(-5,-10) and \newline(−1,5)(-1,5)?\newlineChoose 11 answer:\newline(A) \newline154\frac{15}{4}\newline(B) \newline415\frac{4}{15}\newline(C) \newline−154-\frac{15}{4}\newline(D) \newline−415-\frac{4}{15}
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the slope of the line through (−1,8)(-1,8) and (3,−4)(3,-4)? Choose 11 answer: \newline(A) −13-\frac{1}{3} \newline(B) 13\frac{1}{3} \newline(C) 33 \newline(D) −3-3
Get tutor helpright-arrow

Posted 4 months ago

Question
What is the slope of the line through (2,−2)(2,-2) and (9,3)(9,3)? \newlineChoose 11 answer:\newline(A) 57\frac{5}{7}\newline(B) −57-\frac{5}{7}\newline(C) 75\frac{7}{5}\newline(D) −75-\frac{7}{5}
Get tutor helpright-arrow

Posted 4 months ago

Question
What is the slope of the line through (1,−1)(1,-1) and (5,−7)(5,-7)? Choose 11 answer: (A) −32-\frac{3}{2} (B) 32\frac{3}{2} (C) −23-\frac{2}{3} (D) 23\frac{2}{3}
Get tutor helpright-arrow

Posted 4 months ago

Question
What is the slope of the line through (1,0)(1,0) and (3,8)(3,8)? Choose 11 answer: (A) −14-\frac{1}{4} (B) 44 (C) −4-4 (D) 14\frac{1}{4}
Get tutor helpright-arrow

Posted 4 months ago

Question
What is the slope of the line through (−1,−7)(-1,-7) and (3,9)(3,9)?\newlineChoose 11 answer:\newline(A) 14\frac{1}{4}\newline(B) 44\newline(C) −14-\frac{1}{4}\newline(D) −4-4
Get tutor helpright-arrow

Posted 4 months ago

Question
y+6=5(x−4)y=□ \begin{array}{l}y+6=5(x-4) \\ y=\square\end{array}
Get tutor helpright-arrow

Posted 4 hours ago

View all (15)