AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
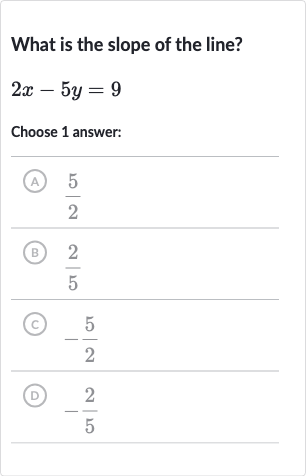
What is the slope of the line?Choose answer:(A) (B) (C) (D)
Full solution
Q. What is the slope of the line?Choose answer:(A) (B) (C) (D)
- Isolating y: We start by isolating y on one side of the equation. We can do this by subtracting from both sides of the equation:
- Dividing both sides: Next, we divide both sides of the equation by to solve for :
- Identifying the slope: Now that we have the equation in slope-intercept form, we can identify the slope. The coefficient of in the equation is the slope of the line.So, the slope is .
