Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

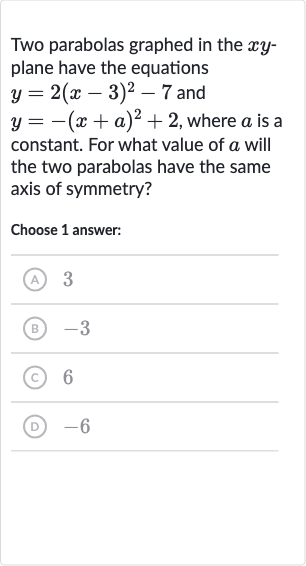
Two parabolas graphed in the xy plane have the equations y=2(x-3)^(2)-7 and y=-(x+a)^(2)+2, where a is a constant. For what value of a will the two parabolas have the same axis of symmetry? Choose 1 answer: (A) 3 (B) -3 (c) 6 (D) -6

Two parabolas graphed in the xy x y plane have the equations y=2(x−3)2−7 y=2(x-3)^{2}-7 and y=−(x+a)2+2 y=-(x+a)^{2}+2 , where a a is a constant. For what value of a a will the two parabolas have the same axis of symmetry?\newlineChoose 11 answer:\newline(A) 33\newline(B) −3-3\newline(C) 66\newline(D) −6-6

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Domain and rangeright chevron icon

Full solution

Q. Two parabolas graphed in the xy x y plane have the equations y=2(x−3)2−7 y=2(x-3)^{2}-7 and y=−(x+a)2+2 y=-(x+a)^{2}+2 , where a a is a constant. For what value of a a will the two parabolas have the same axis of symmetry?\newlineChoose 11 answer:\newline(A) 33\newline(B) −3-3\newline(C) 66\newline(D) −6-6
  1. Finding the axis of symmetry for the first parabola: The axis of symmetry for a parabola in the form y=A(x−h)2+ky = A(x - h)^2 + k is the vertical line x=hx = h. Let's find the axis of symmetry for the first parabola.\newlineThe first parabola is given by y=2(x−3)2−7y = 2(x - 3)^2 - 7.\newlineThe axis of symmetry for this parabola is x=3x = 3.
  2. Finding the axis of symmetry for the second parabola: Now let's find the axis of symmetry for the second parabola.\newlineThe second parabola is given by y=−(x+a)2+2y = -(x + a)^2 + 2.\newlineThe axis of symmetry for this parabola is x=−ax = -a.
  3. Setting the values of h equal: For the two parabolas to have the same axis of symmetry, the values of h from both equations must be equal.\newlineSo we set 33 equal to -a.\newline33 = -a
  4. Solving for aa: Solving for aa, we get:\newlinea=−3a = -3

More problems from Domain and range

Question
What is the domain of this function?\newline(9,–2)(6,–10)(–3,9)(5,2)(9,–2)(6,–10)(–3,9)(5,2)\newlineChoices:\newline(A){–3,5,6,9}(B){–10,–2,2,9}(C){2,5,6,9}(D){–6,–3,5,9}(A)\{–3,5,6,9\}\newline(B)\{–10,–2,2,9\}\newline(C)\{2,5,6,9\}\newline(D)\{–6,–3,5,9\}
Get tutor helpright-arrow

Posted 1 year ago

Question
Look at this set of ordered pairs:\newline(2,14)(2, 14)\newline(10,12)(10, 12)\newline(3,−19)(3, -19)\newlineIs this relation a function?\newlineChoices:\newline[[yes]\text{[[yes]}[no]]\text{[no]]}
Get tutor helpright-arrow

Posted 1 year ago

Question
Use the following function rule to find f(11) f(11) .\newlinef(x)=−10−7x f(x) = -10 - 7x \newlinef(11)= f(11) = _____
Get tutor helpright-arrow

Posted 1 year ago

Question
Find the slope of the line y=−3x−25 y = -3x - \frac{2}{5} .\newlineSimplify your answer and write it as a proper fraction, improper fraction, or integer.\newline_____\_\_\_\_\_
Get tutor helpright-arrow

Posted 1 year ago

Question
A line has a slope of 33 and passes through the point (−2,−10)(-2,-10). Write its equation in slope-intercept form.\newlineWrite your answer using integers, proper fractions, and improper fractions in simplest form.
Get tutor helpright-arrow

Posted 1 year ago

Question
What is the range of this function?\newliney = |x|\newlineChoices:\newlineall real numbers\text{all real numbers}\newline{y∣y≥0}\{y \mid y \geq 0\}\newline{y∣y≤0}\{y \mid y \leq 0\}\newline{y∣y>0}\{y \mid y > 0\}
Get tutor helpright-arrow

Posted 1 year ago

Question
Find g(x) g(x) , where g(x) g(x) is the translation 1 1 unit down of f(x)=∣x∣ f(x) = |x| .\newlineWrite your answer in the form a∣x−h∣+k a|x - h| + k , where a a , h h , and k k are integers.\newlineg(x)= g(x) = ______\newline
Get tutor helpright-arrow

Posted 1 year ago

Question
What is the domain of this function?\newline(8,–1)(7,–11)(–4,10)(4,3)(8,–1)(7,–11)(–4,10)(4,3)\newlineChoices: \newline(A){–4,4,7,8}(A)\{–4,4,7,8\}\newline(B){–11,–1,3,10}(B)\{–11,–1,3,10\}\newline(C){3,4,7,8}(C)\{3,4,7,8\}\newline(D){–7,–4,4,8}(D)\{–7,–4,4,8\}
Get tutor helpright-arrow

Posted 1 year ago

Question
What is the domain of this function?\newline(10, –3)(2, –9)(–5, 8)(3, 1)(10,\,–3)(2,\,–9)(–5,\,8)(3,\,1)\newlineChoices:\newline[{–5,2,3,10}][{–9, –3,1,8}][{1,2,3,10}][{–10, –5,2,3}][\{–5,2,3,10\}][\{–9,\,–3,1,8\}][\{1,2,3,10\}][\{–10,\,–5,2,3\}]
Get tutor helpright-arrow

Posted 1 year ago

Question
What is the domain of this function?\newline(1,–4)(9,–12)(–6,11)(7,5)(1,–4)(9,–12)(–6,11)(7,5)\newlineChoices:(A){–6,1,7,9}\newline\\(A)\{–6,1,7,9\}\newline(B){–12,–4,5,11}(B)\{–12,–4,5,11\}\newline(C{5,1,7,9}(C\{5,1,7,9\}\newline(D){–9,–6,1,7}(D)\{–9,–6,1,7\}
Get tutor helpright-arrow

Posted 1 year ago

View all (377)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant