AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
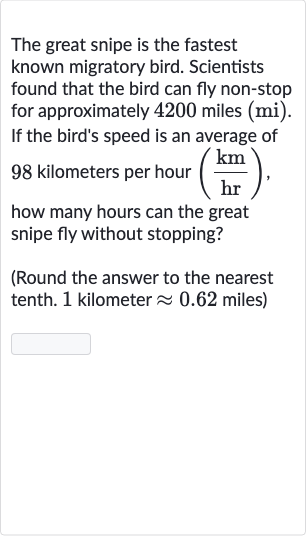
The great snipe is the fastest known migratory bird. Scientists found that the bird can fly non-stop for approximately miles (mi). If the bird's speed is an average of kilometers per hour , how many hours can the great snipe fly without stopping?(Round the answer to the nearest tenth. kilometer miles)
Full solution
Q. The great snipe is the fastest known migratory bird. Scientists found that the bird can fly non-stop for approximately miles (mi). If the bird's speed is an average of kilometers per hour , how many hours can the great snipe fly without stopping?(Round the answer to the nearest tenth. kilometer miles)
- Convert to Kilometers: First, we need to convert the distance from miles to kilometers because the bird's speed is given in kilometers per hour.We know that kilometer is approximately equal to miles. Therefore, to convert miles to kilometers, we use the conversion factor.Calculation: miles kilometers.
- Calculate Distance in Kilometers: Perform the division to find the distance in kilometers.Calculation: kilometers.
- Calculate Time in Hours: Now that we have the distance in kilometers, we can calculate the time it takes for the great snipe to fly this distance at an average speed of kilometers per hour.We use the formula: .Calculation: .
- Find Rounded Time: Perform the division to find the time in hours.Calculation: hours.
- Find Rounded Time: Perform the division to find the time in hours.Calculation: hours. Round the answer to the nearest tenth of an hour as requested.Calculation: hours rounded to the nearest tenth is hours.
More problems from Pythagorean theorem
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
