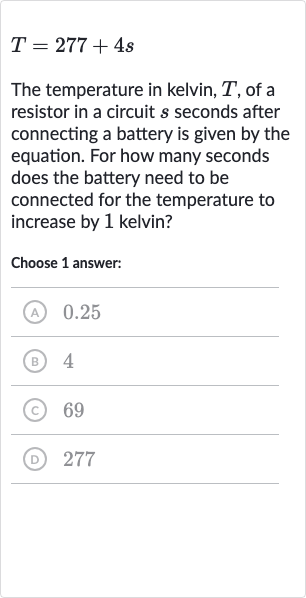
T=277+4s The temperature in kelvin, T, of a resistor in a circuit s seconds after connecting a battery is given by the equation. For how many seconds does the battery need to be connected for the temperature to increase by 1 kelvin? Choose 1 answer: (A) 0.25 (B) 4 (c) 69 (D) 277

Question

T=277+4s The temperature in kelvin,  T, of a resistor in a circuit  s seconds after connecting a battery is given by the equation. For how many seconds does the battery need to be connected for the temperature to increase by 1 kelvin? Choose 1 answer: (A) 0.25 (B) 4 (c) 69 (D) 277

Bytelearn · Accepted Answer

Given Equation: We are given the equation T = 277 + 4s, where T is the temperature in kelvin and s is the time in seconds after connecting a battery. We want to find out how long it takes for the temperature to increase by 1 kelvin. Let's denote the initial temperature as T_initial and the final temperature as T_final. Since the increase is by 1 kelvin, we have T_final = T_initial + 1.Initial Temperature: Let's set up the equation for the initial temperature. We have T_initial = 277 + 4s_initial, where s_initial is the initial time. Since we are looking for the time after the battery is connected, we can assume s_initial to be 0. Therefore, T_initial = 277 + 4(0) = 277.Final Temperature: Now let's set up the equation for the final temperature. We have T_final = 277 + 4s_final, where s_final is the time after which the temperature has increased by 1 kelvin. Since T_final = T_initial + 1, we can write 277 + 4s_final = 277 + 1.Solving for Time: Solving the equation 277 + 4s_final = 278, we subtract 277 from both sides to isolate the term with s_final. This gives us 4s_final = 278 - 277, which simplifies to 4s_final = 1.Finding Time: To find s_final, we divide both sides of the equation by 4. This gives us s_final = 1/4, which is equal to 0.25 seconds.

Full solution

More problems from Write exponential functions: word problems

Related topics