Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Solve for
x.

-7x-50 <= -1quad AND
quad-6x+70 > -2
Choose 1 answer:
(A)
x >= -7
(B)
-7 <= x < 12
(C)
x < 12
(D) There are no solutions
(E) All values of
x are solutions

Solve for $x$ . $\newline$ $-7 x-50 \leq-1 \quad$ AND $\quad-6 x+70>-2$ $\newline$ Choose $1$ answer: $\newline$ (A) $x \geq-7$ $\newline$ (B) $-7 \leq x<12$ $\newline$ (C) $x<12$ $\newline$ (D) There are no solutions $\newline$ (E) All values of $x$ are solutions

View step-by-step help

View step-by-step help

Solve a quadratic equation by factoring

Full solution

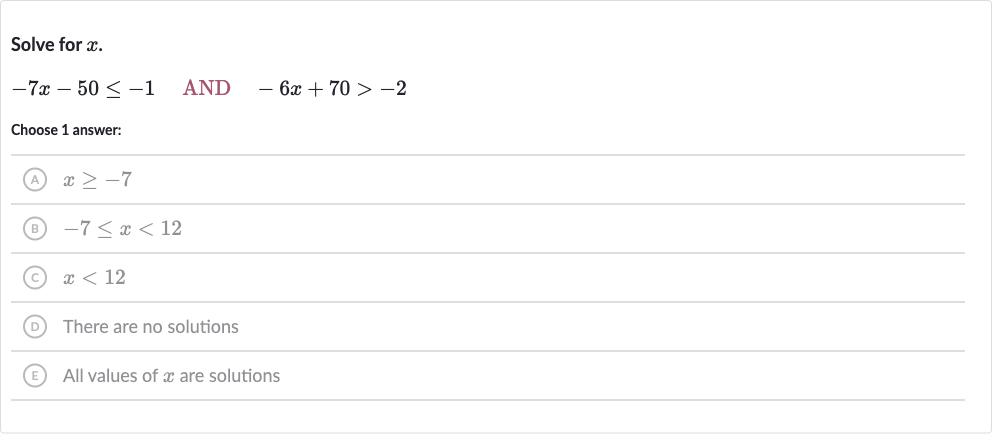
Q. Solve for

x

.

\newline

-7 x-50 \leq-1 \quad

AND

\quad-6 x+70>-2

\newline

Choose

1

answer:

\newline

(A)

x \geq-7

\newline

(B)

-7 \leq x<12

\newline

(C)

x<12

\newline

(D) There are no solutions

\newline

(E) All values of

x

are solutions

Solve First Inequality: Solve the first inequality $-7x - 50 \leq -1$ . To isolate $x$ , we need to add $50$ to both sides of the inequality. $-7x - 50 + 50 \leq -1 + 50$ $-7x \leq 49$ Now, we divide both sides by $-7$ , remembering that dividing by a negative number reverses the inequality sign. $-7x / -7 \geq 49 / -7$ $x \geq -7$
Solve Second Inequality: Solve the second inequality $-6x + 70 > -2$ . $\newline$ First, subtract $70$ from both sides of the inequality. $\newline$ $-6x + 70 - 70 > -2 - 70$ $\newline$ $-6x > -72$ $\newline$ Now, we divide both sides by $-6$ , again remembering to reverse the inequality sign because we are dividing by a negative number. $\newline$ $-6x / -6 < -72 / -6$ $\newline$ $x < 12$
Combine Solutions: Combine the solutions from Step $1$ and Step $2$ to find the range of $x$ that satisfies both inequalities. $\newline$ From Step $1$ , we have $x \geq -7$ . $\newline$ From Step $2$ , we have $x < 12$ . $\newline$ The compound inequality that combines both is $-7 \leq x < 12$ .

More problems from Solve a quadratic equation by factoring

Question

v

\newline

v^2+8v+12=0

\newline

Write each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.

\newline

v=

Posted 5 days ago

Question

u

\newline

u^2 = 9

\newline

Write your answers as integers or as proper or improper fractions in simplest form.

\newline

u =

u =

Posted 3 months ago

Question

Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.

\newline

k^2 - 20k + \_\_\_\_\_

Posted 2 months ago

Question

Solve by completing the square.

\newline

u^2 - 24u - 23 = 0

\newline

Write your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.

\newline

`u` = ________ or `u` =______

Posted 2 months ago

Question

Find the discriminant.

\newline

2q^2 - 9q + 8 = 0

\newline

Posted 2 months ago

Question

Solve the system of equations.

\newline

y = 22x - 38

\newline

y = x^2 + 11x - 14

\newline

Write the coordinates in exact form. Simplify all fractions and radicals.

\newline

(\_,\_)

\newline

(\_,\_)

Posted 2 months ago

Question

a

\newline

(a + 5)(a + 1) = 0

\newline

Write your answers as integers or as proper or improper fractions in simplest form.

\newline

a =

a =

Posted 2 months ago

Question

p=x^{2}-7

. Which equation is equivalent to

(x^{2}-7)^{2}-4x^{2}+28=5

p

1

\newline

p^{2}-4p+23=0

\newline

p^{2}+4p-5=0

\newline

p^{2}-4p-5=0

\newline

p^{2}+4p+23=0

Posted 2 months ago

Question

m=2x+3

. Which equation is equivalent to

(2x+3)^{2}-14x-21=-6

m

1

\newline

m^{2}+7m+6=0

\newline

m^{2}-7m-15=0

\newline

m^{2}-7m+6=0

\newline

m^{2}+7m-15=0

Posted 2 months ago

Question

m=x^{2}+3

. Which equation is equivalent to

(x^{2}+3)^{2}+7x^{2}+21=-10

m

1

\newline

m^{2}-7m+31=0

\newline

m^{2}+7m+31=0

\newline

m^{2}-7m+10=0

\newline

m^{2}+7m+10=0

Posted 3 months ago