Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

M=8(4.5-C) The magnetic field, M, in microtesla, at the center of a loop with a current of C milliamps clockwise is given by the equation. By how many microteslas does the magnetic field change for a 1 milliamp increase in the current? Choose 1 answer: (A) -8 (B) -4.5 (c) 28 (D) 36

M=8(4.5−C) M=8(4.5-C) \newlineThe magnetic field, M M , in microtesla, at the center of a loop with a current of C C milliamps clockwise is given by the equation. By how many microteslas does the magnetic field change for a 11 milliamp increase in the current?\newlineChoose 11 answer:\newline(A) −8-8\newline(B) −4-4.55\newline(C) 2828\newline(D) 3636

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Domain and rangeright chevron icon

Full solution

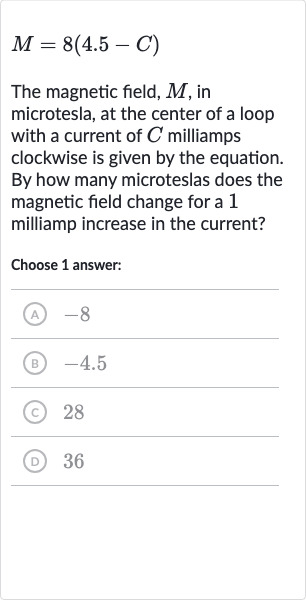
Q. M=8(4.5−C) M=8(4.5-C) \newlineThe magnetic field, M M , in microtesla, at the center of a loop with a current of C C milliamps clockwise is given by the equation. By how many microteslas does the magnetic field change for a 11 milliamp increase in the current?\newlineChoose 11 answer:\newline(A) −8-8\newline(B) −4-4.55\newline(C) 2828\newline(D) 3636
  1. Understand the equation: Understand the given equation.\newlineThe equation M=8(4.5−C)M = 8(4.5 - C) describes the magnetic field MM in microteslas as a function of the current CC in milliamps. We need to find out how much the magnetic field changes when the current increases by 11 milliamp.
  2. Calculate change in field: Calculate the change in the magnetic field for a 11 milliamp increase in current.\newlineLet's first calculate the magnetic field for a current CC. Then we will calculate the magnetic field for a current C+1C + 1 milliamp and find the difference between the two.
  3. Calculate field for C: Calculate the magnetic field for the current CC. Using the given equation, the magnetic field for current CC is M=8(4.5−C)M = 8(4.5 - C).
  4. Calculate field for C+1C+1: Calculate the magnetic field for the current C+1C + 1 milliamp.\newlineFor a current of C+1C + 1 milliamps, the magnetic field will be M′=8(4.5−(C+1))M' = 8(4.5 - (C + 1)).
  5. Simplify expression for M′M': Simplify the expression for M′M'.M′=8(4.5−C−1)=8(3.5−C)M' = 8(4.5 - C - 1) = 8(3.5 - C).
  6. Find change in field: Find the change in the magnetic field.\newlineThe change in the magnetic field ΔM\Delta M is the difference between M′M' and MM.\newlineΔM=M′−M=8(3.5−C)−8(4.5−C).\Delta M = M' - M = 8(3.5 - C) - 8(4.5 - C).
  7. Simplify expression for ΔM\Delta M: Simplify the expression for ΔM\Delta M. \newlineΔM=8(3.5−C)−8(4.5−C)=8×3.5−8C−8×4.5+8C\Delta M = 8(3.5 - C) - 8(4.5 - C) = 8 \times 3.5 - 8C - 8 \times 4.5 + 8C.
  8. Cancel out terms with C: Cancel out the terms with C.\newlineSince −8C-8C and +8C+8C are on opposite sides of the subtraction, they cancel each other out.\newlineΔM=8×3.5−8×4.5=28−36\Delta M = 8 \times 3.5 - 8 \times 4.5 = 28 - 36.
  9. Calculate final change: Calculate the final change in the magnetic field. \newlineΔM=28−36=−8\Delta M = 28 - 36 = -8 microteslas.

More problems from Domain and range

Question
What is the domain of this function?\newline(9,–2)(6,–10)(–3,9)(5,2)(9,–2)(6,–10)(–3,9)(5,2)\newlineChoices:\newline(A){–3,5,6,9}(B){–10,–2,2,9}(C){2,5,6,9}(D){–6,–3,5,9}(A)\{–3,5,6,9\}\newline(B)\{–10,–2,2,9\}\newline(C)\{2,5,6,9\}\newline(D)\{–6,–3,5,9\}
Get tutor helpright-arrow

Posted 1 year ago

Question
Look at this set of ordered pairs:\newline(2,14)(2, 14)\newline(10,12)(10, 12)\newline(3,−19)(3, -19)\newlineIs this relation a function?\newlineChoices:\newline[[yes]\text{[[yes]}[no]]\text{[no]]}
Get tutor helpright-arrow

Posted 1 year ago

Question
Use the following function rule to find f(11) f(11) .\newlinef(x)=−10−7x f(x) = -10 - 7x \newlinef(11)= f(11) = _____
Get tutor helpright-arrow

Posted 1 year ago

Question
Find the slope of the line y=−3x−25 y = -3x - \frac{2}{5} .\newlineSimplify your answer and write it as a proper fraction, improper fraction, or integer.\newline_____\_\_\_\_\_
Get tutor helpright-arrow

Posted 1 year ago

Question
A line has a slope of 33 and passes through the point (−2,−10)(-2,-10). Write its equation in slope-intercept form.\newlineWrite your answer using integers, proper fractions, and improper fractions in simplest form.
Get tutor helpright-arrow

Posted 1 year ago

Question
What is the range of this function?\newliney = |x|\newlineChoices:\newlineall real numbers\text{all real numbers}\newline{y∣y≥0}\{y \mid y \geq 0\}\newline{y∣y≤0}\{y \mid y \leq 0\}\newline{y∣y>0}\{y \mid y > 0\}
Get tutor helpright-arrow

Posted 1 year ago

Question
Find g(x) g(x) , where g(x) g(x) is the translation 1 1 unit down of f(x)=∣x∣ f(x) = |x| .\newlineWrite your answer in the form a∣x−h∣+k a|x - h| + k , where a a , h h , and k k are integers.\newlineg(x)= g(x) = ______\newline
Get tutor helpright-arrow

Posted 1 year ago

Question
What is the domain of this function?\newline(8,–1)(7,–11)(–4,10)(4,3)(8,–1)(7,–11)(–4,10)(4,3)\newlineChoices: \newline(A){–4,4,7,8}(A)\{–4,4,7,8\}\newline(B){–11,–1,3,10}(B)\{–11,–1,3,10\}\newline(C){3,4,7,8}(C)\{3,4,7,8\}\newline(D){–7,–4,4,8}(D)\{–7,–4,4,8\}
Get tutor helpright-arrow

Posted 1 year ago

Question
What is the domain of this function?\newline(10, –3)(2, –9)(–5, 8)(3, 1)(10,\,–3)(2,\,–9)(–5,\,8)(3,\,1)\newlineChoices:\newline[{–5,2,3,10}][{–9, –3,1,8}][{1,2,3,10}][{–10, –5,2,3}][\{–5,2,3,10\}][\{–9,\,–3,1,8\}][\{1,2,3,10\}][\{–10,\,–5,2,3\}]
Get tutor helpright-arrow

Posted 1 year ago

Question
What is the domain of this function?\newline(1,–4)(9,–12)(–6,11)(7,5)(1,–4)(9,–12)(–6,11)(7,5)\newlineChoices:(A){–6,1,7,9}\newline\\(A)\{–6,1,7,9\}\newline(B){–12,–4,5,11}(B)\{–12,–4,5,11\}\newline(C{5,1,7,9}(C\{5,1,7,9\}\newline(D){–9,–6,1,7}(D)\{–9,–6,1,7\}
Get tutor helpright-arrow

Posted 1 year ago

View all (377)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant