Full solution
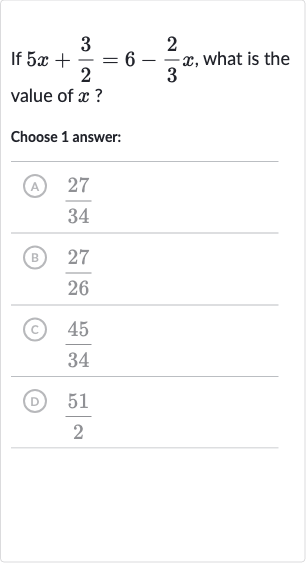
Q. If , what is the value of ?Choose answer:(A) (B) (C) (D)
- Write equation: Write down the given equation.We have the equation .
- Clear fractions: Clear the fractions by finding a common denominator for the terms with fractions.The common denominator for and is . Multiply every term in the equation by to eliminate the fractions.$\(6\) \times (\(5\)x) + \(6\) \times \left(\frac{\(3\)}{\(2\)}\right) = \(6\) \times \(6\) - \(6\) \times \left(\frac{\(2\)}{\(3\)}\right)x
- Multiply by common denominator: Simplify the equation by performing the multiplications. \(30x + 9 = 36 - 4x\)
- Simplify equation: Move all \(x\) terms to one side of the equation and constants to the other side.\(\newline\)Add \(4x\) to both sides to get all \(x\) terms on one side.\(\newline\)\(30x + 4x + 9 = 36 - 4x + 4x\)
- Rearrange terms: Combine like terms. \(34x + 9 = 36\)
- Combine like terms: Subtract \(9\) from both sides to isolate the term with \(x\).\(\newline\)\[34x + 9 - 9 = 36 - 9\]
- Isolate x term: Simplify the equation. \(34x = 27\)
- Simplify equation: Divide both sides by \(34\) to solve for \(x\).\(\newline\)\(x = \frac{27}{34}\)