Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate.

(2)/(5)÷(8)/(5)=

Evaluate. $\newline$ $\frac{2}{5} \div \frac{8}{5}=$

View step-by-step help

View step-by-step help

Add, subtract, multiply, and divide integers

Full solution

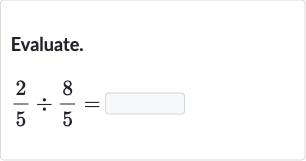
Q. Evaluate.

\newline

\frac{2}{5} \div \frac{8}{5}=

Understanding division between fractions: Understand the operation of division between two fractions. $\newline$ To divide one fraction by another, you multiply the first fraction by the reciprocal of the second fraction. The reciprocal of a fraction is obtained by swapping its numerator and denominator.
Finding the reciprocal of the second fraction: Find the reciprocal of the second fraction. $\newline$ The second fraction is $(\frac{8}{5})$ . Its reciprocal is $(\frac{5}{8})$ .
Multiplying the first fraction by the reciprocal: Multiply the first fraction by the reciprocal of the second fraction. $\newline$ Now we multiply $(\frac{2}{5})$ by $(\frac{5}{8})$ . $\newline$ $(\frac{2}{5}) \times (\frac{5}{8}) = \frac{2 \times 5}{5 \times 8}$
Performing the multiplication: Perform the multiplication. $\newline$ Now we multiply the numerators together and the denominators together. $\newline$ $(2 \times 5)/(5 \times 8) = 10/40$
Simplifying the fraction: Simplify the fraction. $\newline$ The fraction $\frac{10}{40}$ can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is $10$ . $\newline$ $\frac{10}{40} = \frac{10/10}{40/10} = \frac{1}{4}$

More problems from Add, subtract, multiply, and divide integers

Question

Write an expression to represent:

7

minus the product of

3

x

Posted 4 months ago

Question

Write an expression to represent:

9

minus the quotient of

2

x

Posted 4 months ago

Question

Write an expression to represent:

\newline

2

times the sum of

5

x

Posted 4 months ago

Question

\newline

\frac{2}{7} \div \frac{8}{3}=

Posted 4 months ago

Question

\newline

\frac{8}{5} \div \frac{7}{8}=

Posted 4 months ago

Question

\newline

\frac{1}{4} \div \frac{8}{3}=

Posted 4 months ago

Question

\newline

\frac{2}{7} \div \frac{4}{9}=

Posted 4 months ago

Question

\newline

\frac{2}{5} \div \frac{1}{7}=

Posted 4 months ago

Question

\newline

\frac{4}{7} \div \frac{7}{2}=

Posted 4 months ago

Question

He predicts that the relationship between

N

, the number of branches on the tree, and

t

years, since the tree was planted can be modeled by the following equation.

N = 5 \cdot 100.3^t

According to Takumi's model, in how many years will the tree have

100

branches? Give an exact answer expressed as a base-

10

Posted 2 hours ago