A circle in the $x y$ -plane has its center on the line $y=1$ . If the point $(2,-3)$ lies on the circle and the radius is $4$ , which of the following could be the center of the circle? $\newline$ Choose $1$ answer: $\newline$ (A) $(2,1)$ $\newline$ (B) $(2,-3)$ $\newline$ (C) $(4,1)$ $\newline$ (D) $(-4,1)$

View step-by-step help

Home

Math Problems

Grade 8

Write a linear equation from a slope and a point

Full solution

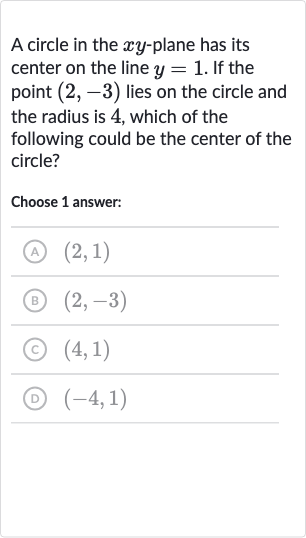
Q. A circle in the

x y

-plane has its center on the line

y=1

. If the point

(2,-3)

lies on the circle and the radius is

4

, which of the following could be the center of the circle?

\newline

Choose

1

answer:

\newline

(A)

(2,1)

\newline

(B)

(2,-3)

\newline

(C)

(4,1)

\newline

(D)

(-4,1)

Problem and Given Information: Understand the problem and the given information. $\newline$ We are given that the center of the circle lies on the line $y=1$ , which means that the $y$ -coordinate of the center is $1$ . We also know that the circle passes through the point $(2,-3)$ and has a radius of $4$ units.
Distance Formula for x-coordinate: Use the distance formula to find the possible x-coordinates of the center. $\newline$ The distance formula is $d = \sqrt{((x_2 - x_1)^2 + (y_2 - y_1)^2)}$ , where $d$ is the distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ . Here, we know the distance (radius) is $4$ , one point is $(2,-3)$ , and the other point (the center) has a y-coordinate of $1$ . We need to find the x-coordinate of the center.
Solving for x-coordinate: Plug in the known values into the distance formula and solve for the x-coordinate. $\newline$ Let the x-coordinate of the center be $x$ . Then we have: $\newline$ $4 = \sqrt{((x - 2)^2 + (1 - (-3))^2)}$ $\newline$ $16 = (x - 2)^2 + (1 + 3)^2$ $\newline$ $16 = (x - 2)^2 + 16$ $\newline$ $0 = (x - 2)^2$ $\newline$ $x - 2 = 0$ $\newline$ $x = $2$
Checking Possible Centers: Check the possible centers against the given options.$\newline$We have found that the x-coordinate of the center is $2$, and we know the y-coordinate is $1$ (since the center lies on the line $y=1$). Therefore, the center of the circle is $(2,1)$.
Matching Center with Answer Choices: Match the found center with the given answer choices.$\newline$The center $(2,1)$ matches with answer choice $(A)$.