Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

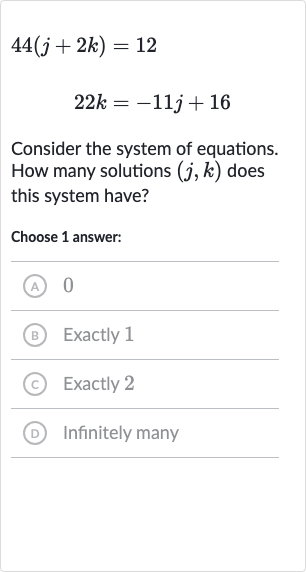
44(j+2k)=12 22 k=-11 j+16 Consider the system of equations. How many solutions (j,k) does this system have? Choose 1 answer: (A) 0 (B) Exactly 1 (c) Exactly 2 (D) Infinitely many

44(j+2k)=12 44(j+2 k)=12 \newline22k=−11j+16 22 k=-11 j+16 \newlineConsider the system of equations. How many solutions (j,k) (j, k) does this system have?\newlineChoose 11 answer:\newline(A) 00\newline(B) Exactly 11\newline(C) Exactly 22\newline(D) Infinitely many

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Find the number of solutions to a system of equationsright chevron icon

Full solution

Q. 44(j+2k)=12 44(j+2 k)=12 \newline22k=−11j+16 22 k=-11 j+16 \newlineConsider the system of equations. How many solutions (j,k) (j, k) does this system have?\newlineChoose 11 answer:\newline(A) 00\newline(B) Exactly 11\newline(C) Exactly 22\newline(D) Infinitely many
  1. Simplify the first equation: Simplify the first equation.\newlineThe first equation is 44(j+2k)=1244(j+2k)=12. To simplify, divide both sides by 4444 to isolate (j+2k)(j+2k).\newlinej+2k=1244j + 2k = \frac{12}{44}\newlinej+2k=311j + 2k = \frac{3}{11}
  2. Simplify the second equation: Simplify the second equation.\newlineThe second equation is 22k=−11j+1622k = -11j + 16. To simplify, divide both sides by 2222 to isolate kk.\newlinek=−11j+1622k = \frac{-11j + 16}{22}\newlinek=−12j+811k = -\frac{1}{2} j + \frac{8}{11}
  3. Compare the two simplified equations: Compare the two simplified equations.\newlineWe have j+2k=311j + 2k = \frac{3}{11} and k=−12j+811k = -\frac{1}{2} j + \frac{8}{11}. We can substitute the expression for kk from the second equation into the first equation to solve for jj.\newlinej+2(−12j+811)=311j + 2\left(-\frac{1}{2} j + \frac{8}{11}\right) = \frac{3}{11}
  4. Solve for j: Solve for j.\newlineDistribute the 22 in the first equation:\newlinej−j+1611=311j - j + \frac{16}{11} = \frac{3}{11}\newlineNotice that j−jj - j cancels out, leaving us with:\newline1611=311\frac{16}{11} = \frac{3}{11}
  5. Check for consistency: Check for consistency.\newlineWe see that 1611\frac{16}{11} does not equal 311\frac{3}{11}. This means that there is no value of jj that can satisfy both equations simultaneously.
  6. Determine the number of solutions: Determine the number of solutions.\newlineSince there is no value of jj that can satisfy both equations, there is no solution to the system of equations.

More problems from Find the number of solutions to a system of equations

Question
Solve using elimination.\newlinex+6y=−15x + 6y = -15\newline−2x+6y=12-2x + 6y = 12\newline(_,_)(\_,\_)
Get tutor helpright-arrow

Posted 3 months ago

Question
Is (1,1)(1,1) a solution to this system of equations?\newline8x+y=98x + y = 9\newline6x+12y=186x + 12y = 18\newlineChoices:\newline[[yes]\newline[no]]
Get tutor helpright-arrow

Posted 2 months ago

Question
How many solutions does the system of equations below have?\newliney = x − 77\newliney = x − 77\newlineChoices:\newline[A]no solution\text{[A]no solution}\newline[B]one solution\text{[B]one solution}\newline[C]infinitely many solutions\text{[C]infinitely many solutions}
Get tutor helpright-arrow

Posted 2 months ago

Question
Which describes the system of equations below?\newliney=17x−10y = \frac{1}{7}x - 10\newliney=17x−10y = \frac{1}{7}x - 10\newlineChoices:\newline[A]consistent and independent\text{[A]consistent and independent}\newline[B]consistent and dependent\text{[B]consistent and dependent}\newline[C]inconsistent\text{[C]inconsistent}
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve using substitution.\newliney=−5y = -5\newline−4x+3y=17-4x + 3y = 17\newline(_____, _____)
Get tutor helpright-arrow

Posted 2 months ago

Question
Write a system of equations to describe the situation below, solve using substitution, and fill in the blanks.\newlineLast Wednesday, two friends met up after school to read the book they were both assigned in Literature class. Bryan can read 22 pages per minute, and he had already read 9898 pages. Jayla, who has a reading speed of 33 pages per minute, had read 4848 pages. Eventually they had read the same number of pages. How long did that take? How many pages had each of them read?\newlineAfter ____\_\_\_\_ minutes, Bryan and Jayla had each read ____\_\_\_\_ pages.
Get tutor helpright-arrow

Posted 2 months ago

Question
Write a system of equations to describe the situation below, solve using elimination, and fill in the blanks.\newlineAt the Castroville Ice Cream Parlor, one group of friends ordered 11 small serving of ice cream and 33 large servings of ice cream for 2020. Another group of friends ordered 11 small serving of ice cream and 44 large servings of ice cream for 2626. How much does the ice cream cost?\newlineThe ice cream costs `\$`_____ for a small serving and `\$`_____ for a large serving.
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve.\newliney=−1y = -1\newline−2x−4y=8-2x - 4y = 8\newline(_____ , _____)
Get tutor helpright-arrow

Posted 2 months ago

Question
Write a system of equations to describe the situation below, solve using any method, and fill in the blanks.\newlineThere are two mystery numbers. The sum of 33 times the first number and 33 times the second number is −18-18. The sum of 22 times the first number and 33 times the second number is −13-13. What are the two numbers?\newlineThe first number is ______ , and the second number is ______.
Get tutor helpright-arrow

Posted 2 months ago

Question
A teacher purchased 300300 colored pencils for an upcoming project. The pencils she ordered come in packs of 2020 and packs of 3030. She ordered 1414 packs in all. Write a system of equations to find the number of 2020-pencil packs (x)(x) and 3030-pencil packs (y)(y) the art teacher ordered.
Get tutor helpright-arrow

Posted 3 months ago

View all (96)