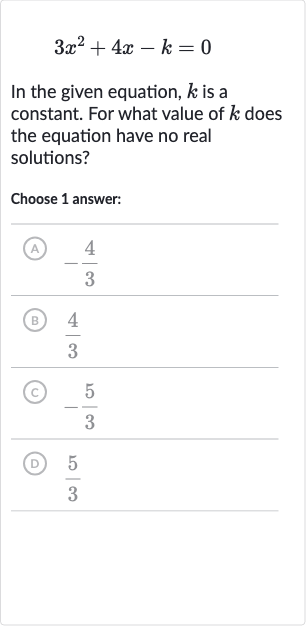
Full solution
Q. In the given equation, is a constant. For what value of does the equation have no real solutions?Choose answer:(A) (B) (C) (D)
- Identify Equation: The given equation is . Here, , , and . We will calculate the discriminant using these values.The discriminant () is .
- Calculate Discriminant: Now we calculate the discriminant: . For the equation to have no real solutions, the discriminant must be less than zero. Therefore, we set up the inequality 16 + 12k < 0.
- Set Up Inequality: We solve the inequality for : 12k < -16.Divide both sides by to isolate : k < -\frac{16}{12}.Simplify the fraction: k < -\frac{4}{3}.
- Solve for : The value of that makes the equation have no real solutions is any number less than . Looking at the answer choices, we see that the value that fits this condition is (C) , since is less than .