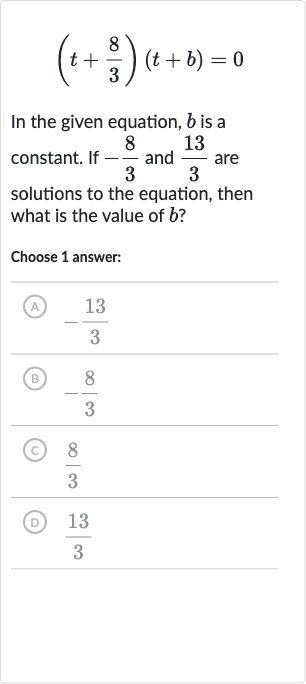
(t+(8)/(3))(t+b)=0 In the given equation, b is a constant. If -(8)/(3) and (13)/(3) are solutions to the equation, then what is the value of b ? Choose 1 answer: (A) -(13)/(3) (B) -(8)/(3) (C) (8)/(3) (D) (13)/(3)

Question

(t+(8)/(3))(t+b)=0 In the given equation,  b is a constant. If  -(8)/(3) and  (13)/(3) are solutions to the equation, then what is the value of  b ? Choose 1 answer: (A)  -(13)/(3) (B)  -(8)/(3) (C)  (8)/(3) (D)  (13)/(3)

Bytelearn · Accepted Answer

Given Equation Analysis: We are given the equation (t+(8)/(3))(t+b)=0 and told that -(8)/(3) and (13)/(3) are solutions to this equation. This means that when we substitute t with either -(8)/(3) or (13)/(3), the equation should be satisfied.Substitute First Solution: First, let's substitute t with the first solution -(8)/(3) into the equation and see if it satisfies the equation. (t+(8)/(3))(t+b)=0 Substitute t = -(8)/(3): ((-(8)/(3))+(8)/(3))((-(8)/(3))+b)=0Simplify First Substitution: Simplify the expression: (0)(((8)/(3))+b)=0 Since anything multiplied by 0 is 0, this part of the equation is satisfied regardless of the value of b.Substitute Second Solution: Now, let's substitute t with the second solution (13)/(3) into the equation. (t+(8)/(3))(t+b)=0 Substitute t = (13)/(3): (((13)/(3))+(8)/(3))(((13)/(3))+b)=0Simplify Second Substitution: Simplify the expression: ((21)/(3))(((13)/(3))+b)=0 Since (21)/(3) is 7 and 7 is not equal to 0, the only way for the product to be 0 is if the second factor is 0.Solve for b: Set the second factor equal to zero and solve for b: ((13)/(3))+b=0 b = -(13)/(3)Final Answer: We have found the value of b that satisfies the equation when t is (13)/(3). Since the problem asks for the value of b, we have our answer.

Full solution

More problems from Domain and range

Related topics