Full solution
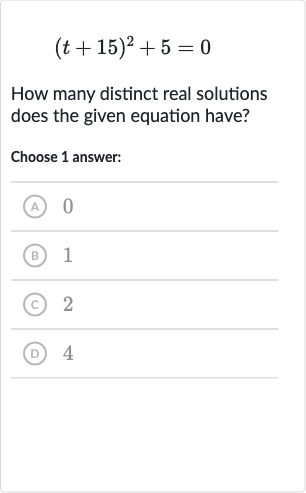
Q. How many distinct real solutions does the given equation have?Choose answer:(A) (B) (C) (D)
- Given equation: We are given the equation and we need to find the number of distinct real solutions.First, we will try to isolate the squared term by subtracting from both sides of the equation.
- Isolating the squared term: Now, we observe that the left side of the equation is a square of a real number, which can never be negative since squaring any real number always gives a non-negative result.Therefore, cannot equal for any real number .This means there are no real solutions to the equation.