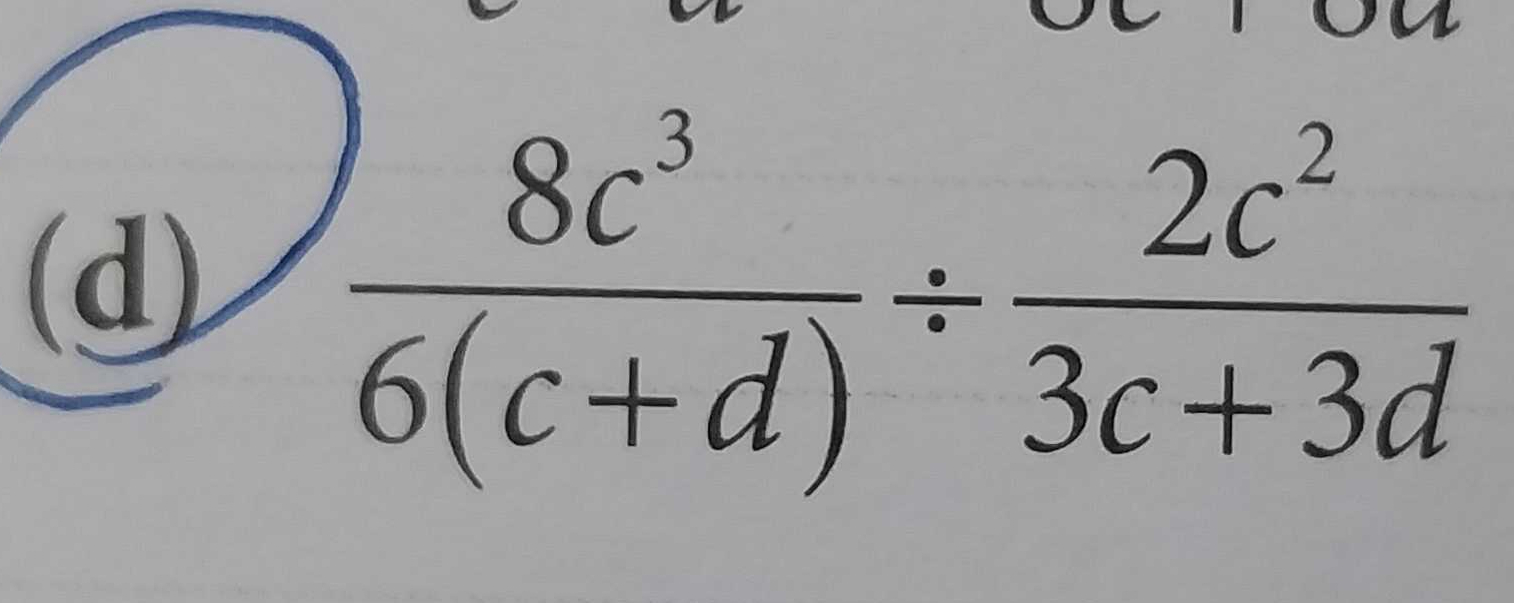Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

(d)
(8c^(3))/(6(c+d))÷(2c^(2))/(3c+3d)

(d) $\frac{8 c^{3}}{6(c+d)} \div \frac{2 c^{2}}{3 c+3 d}$

View step-by-step help

View step-by-step help

Operations with rational exponents

Full solution

Q. (d)

\frac{8 c^{3}}{6(c+d)} \div \frac{2 c^{2}}{3 c+3 d}

Identify & Rewrite Division: Identify the given expression and rewrite the division as multiplication by the reciprocal of the second fraction. $\newline$ $(8c^{3})/(6(c+d)) \div (2c^{2})/(3c+3d) = (8c^{3})/(6(c+d)) \times (3c+3d)/(2c^{2})$
Simplify Coefficients & Variables: Simplify the coefficients and variables where possible. $\newline$ First, notice that $8$ and $6$ can be simplified by dividing both by $2$ , and $3c+3d$ can be factored to $3(c+d)$ . $\newline$ $\frac{8c^{3}}{6(c+d)} \times \frac{3c+3d}{2c^{2}} = \frac{4c^{3}}{3(c+d)} \times \frac{3(c+d)}{c^{2}}$
Cancel Common Terms: Cancel out the common terms in the numerator and the denominator. $\newline$ The $(c+d)$ terms cancel out, and we are left with: $\newline$ $\frac{4c^{3}}{3(c+d)} \times \frac{3(c+d)}{c^{2}} = \frac{4c^{3}}{1} \times \frac{1}{c^{2}} = \frac{4c^{3}}{c^{2}}$
Simplify Remaining Expression: Simplify the remaining expression by subtracting the exponents of $c$ . When dividing like bases, subtract the exponents: $\frac{c^{3}}{c^{2}} = c^{3-2} = c^{1} = c$ . $\frac{4c^{3}}{c^{2}} = 4c$

More problems from Operations with rational exponents

Question

f(x)=\frac{6 x+5}{2-\sqrt{14+5 x}}

\newline

We want to find

\lim _{x \rightarrow-2} f(x)

\newline

What happens when we use direct substitution?

\newline

1

\newline

(A) The limit exists, and we found it!

\newline

(B) The limit doesn't exist (probably an asymptote).

\newline

(C) The result is indeterminate.

Posted 4 months ago

Question

x^{4}+y^{2}=17

\newline

What is the value of

\frac{d^{2} y}{d x^{2}}

(-2,1)

\newline

Give an exact number.

Posted 3 months ago

Question

What is the area of the region bound by the graphs of

f(x)=\sqrt{x-2}, g(x)=14-x

x=2

\newline

1

\newline

\frac{19}{6}

\newline

\frac{99}{2}

\newline

\frac{151}{2}

\newline

\frac{45}{2}

Posted 2 months ago

Question

g(x)=x^{\frac{4}{3}}

\newline

g^{\prime}(27)=

Posted 2 months ago

Question

\ln \left(\frac{1}{\sqrt{e}}\right)

\newline

Posted 3 months ago

Question

\ln \left(\frac{1}{e}\right)

\newline

Posted 3 months ago

Question

y=(\sin^{-1}(5x^{2}))^{3}

Posted 3 months ago

Question

\left(10x^{3}-5x^{2}-6x\right)\div\left(2x^{2}\right)

Posted 3 months ago

Question

y=\cos^{4}x\sin^{4}x

Posted 3 months ago

Question

\frac{3}{5}-\frac{3}{10}

Posted 3 months ago