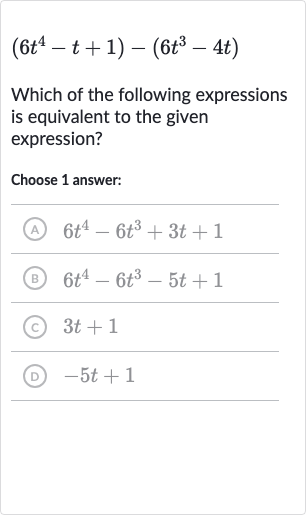
Full solution
Q. Which of the following expressions is equivalent to the given expression?Choose answer:(A) (B) (C) (D)
- Subtracting Polynomials: We need to subtract the second polynomial from the first one. To do this, we distribute the negative sign across the terms in the second polynomial and then combine like terms. becomes .
- Combining Like Terms: Now, we combine like terms. There are no other or terms, so they remain as they are. The terms are and , which combine to . The constant term is .So, the expression becomes .
- Checking the Expression: We check the expression to ensure there are no other like terms that can be combined and that all signs have been correctly distributed. is the simplified form, and there are no further like terms to combine.